نقش قابلتوجه حفرههای رزونانس بلور فوتونی در فیلترهای قابل تنظیم ارتباطی WDM و DWDM
چکیده :
یک روش فیلتر بلور فوتونی با استفاده از حفرههای رزونانس در ساختارهای دوبعدی مناسب برای کاربردهای ارتباطی WDM و DWDM، پیشنهادشده است. برای طراحی ساختار، حرکت نقصهای شبکه بهعنوان حفره رزونانس استفاده میشود. تنظیم طولموج موردنظر با مشخصات مطابق با استاندارد ITU-T نشان دادهشده است. با تغییر ویژگیهایی مانند شعاع نقصها، فاصله آنها از یکدیگر و محل نقص، یک فیلتر نوری کامپکت مناسب برای مدارهای مجتمع نوری پیشنهادشده است. همچنین اثر ترکیبی، شعاع متغیر نقصها و فاصله آنها از یکدیگر باعث ایجاد ویژگیهای جالب میشود.
مقدمه
نقش مهم فیلترهای نوری برای شبکههای ارتباطی نوری، در دهههای اخیر تعیینشده است. فیلترهای نوری دستگاههای بسیار مهم برای دستگاههای ارتباطی نوری هستند [۱]. با استفاده از مالتی پلکس بر اساس تقسیم طولموج[۱] (ﻫﻤﺘﺎﻓﺘﮕﺮی ﺗﻘﺴﯿﻢ طولموج ) (WDM) و مالتی پلکس بر اساس تقسیم طولموج متراکم[۲] (ﻫﻤﺘﺎﻓﺘﮕﺮی چگال ﺗﻘﺴﯿﻢ طولموج) (DWDM) میتوانیم ظرفیت یک فیبر نوری واحد را افزایش دهیم بهطوریکه یک فیبر نوری میتواند کانالهای متعدد (۴، ۸ یا بیشتر) را در طولموجهای مرکزی مختلف حمل کند. با یک فیلتر نوری میتوانید کانال نوری موردنظر را انتخاب کنید [۲-۵]. درواقع با بهکارگیری فیلترهای نوری، میتوان کانالهای نوری فاصلهدار بسیار نزدیک را بدون استفاده از دستگاههای الکترونیکی جدا کرد [۶-۸]. طبق استانداردهای DWDM طولموجهای کاربردی برای کاربردهای ارتباطی نوری در محدوده ۱۵۵۰ تا ۱۶۰۰ نانومتر میباشند و فاصله کانال بین دو کانال مجاور نباید بیش از ۱ نانومتر باشد.
اخیراً انواع مختلفی از فیلترهای نوری مانند توریهای صفحهای، تداخلسنجهای[۳] Fabry–Perot، فیبر توری Bragg، توریهای موجبر مرتبشده، تداخلسنجهای Mach–Zehnder و فیلترهای تداخل دیالکتریک فیلم نازک، گزارششده است [۹]. تمام فیلترهای ذکرشده، ساختارهای خوبی دارند، اما نداشتن قابلیت ادغام به ابعاد فوقالعاده کوچک مناسب برای مدارهای مجتمع نوری، مشکل ساخت فیلترهای باند باریک بافاصله کانونی کوچک و مشکل تنظیم آنها، دلایل محدودکننده کاربرد آنها در WDM و DWDM نوری شبکههای ارتباطی میباشد.
طراحی دستگاههای خیلی کوچک که مناسب همهی مدارهای نوری است همیشه برای محققان اپتیک و فوتونیک بسیار جالب است. این ویژگی قابلتوجه – اندازه کوچک – به علت محصور شوندگی کمنور در فضای کوچک، محدودشده است [۱۰-۱۳]. اما بلورهای فوتونی به علت توزیع دورهای آنها از ضریبهای شکست، این مشکل را حل کردهاند. مهمترین ویژگی این ساختارها، که آنها را برای محققان بسیار جالب ساخته است، باند گپ فوتونی[۴] (PBG) آنها است. در تعریف، باند گپ فوتونی، یک گسترهی طولموج در ساختار باند بلورهای فوتونی[۵] (PhCs) است که انتشار هر موج الکترومغناطیسی ممنوع است. بهعبارتدیگر اگر یک موج نوری که طولموج آن در PBG بلورهای فوتونی به سطح آن رسیده باشد، قادر به انتشار آن نیست و بهطور کامل از سطح آن منعکس میشود. با توجه به عملکرد توزیع شاخصهای انکسار، بلورهای فوتونی به سه دسته تقسیم میشوند: بلورهای فوتونی ۱ بعدی، بلورهای فوتونی ۲ بعدی و بلورهای فوتونی سهبعدی. بلورهای فوتونی ۱ بعدی، که همچنین چندلایه نیز نامیده میشود یک PBG کامل ندارد و همچنین ساخت بلورهای فوتونی ۳ بعدی، به دلیل ثابتهای شبکه کوچک آنها، بسیار دشوار است. اما بلورهای فوتونی ۲ بعدی دارای PBG کامل هستند و ساخت آنها آسانتر از بلورهای فوتونی ۳ بعدی است. بنابراین آنها برای پژوهشگران مطلوبتر است. تا آنجا که ما میدانیم، بلورهای فوتونی ۲ بعدی از حفرههای هوایی در یک بستر دیالکتریک و یا میلههای استوانهای از ماده دیالکتریک غوطهور در هوا تشکیلشده است. با تغییر ثابت شبکه، شعاع میلهها و شاخص انکسار دیالکتریک را میتوانPBG بلورهای فوتونی را تنظیم کرد [۱۴،۱۵]. در بلورهای فوتونی ۲ بعدی ما میتوانیم با حذف یک ردیف میلهها یک موجبر ایجاد کنیم که اگر یک موج نوری که طولموج آن در PBG بلور فوتونی وارد این موجبر شود، میتواند بدون پراکندگی در ساختار، از طریق موجبر عبور کند. انتشاردهندههای اپتیکی [۱۶]، فیلترهای نوری [۱۷]، سوئیچهای نوری [۱۸]، اسپیلیتور ها (شکافندههای) نوری [۱۹]، و دستگاههای دی مالتی پلکسر (انشعاب گر) اپتیکی [۲۰،۲۱] نمونههایی از دستگاههای مبتنی بر بلورهای فوتونی هستند. فیلترهای نوری یکی از مهمترین کاربردهای بلورهای فوتونی برای طراحی دستگاههایی هستند که برای دستگاههای WDM و DWDM مناسب هستند. هترو ساختارهای مبتنی بر بلورهای فوتونی در شکلهای مختلف مورداستفاده قرارگرفته است: استفاده از رزونانس دهندههای حلقهها [۲۲] در دی مالتی پلکسر مبتنی بر بلور فوتونی [۲۳]، در دو کانال طولموج دی مالتی پلکسر [۲۴] در فیلتر قطره کانال قابل تنظیم که توسط اثرات الکترو-اپتیک در مواد انکسار دوتایی [ ۲۵] و در فیلترهای مبتنی بر سوپر – منشور شاخص انکسار منفی[۲۶،۲۷].
تمام چیزی که یک فیلتر نوری انجام میدهد، انتخاب طولموج ویژه در میان طولموجهای بسیار است. در مقالات، روشهای مختلفی برای انتخاب طولموج وجود دارد. یکی از فیلتر فزود – فرود[۶] است که شامل دو خط نقص بهعنوان ورودی و خروجی افت گذرگاه و یک حفره رزونانس بین آنها است. انتخاب طولموج توسط این حفره انجام میشود. موج از پورت ورودی واردشده سپس تعدادی از طولموجها از طریق حفره به موجبر فرود شده، کوپل شده و سپس به پورت خروجی منتقل میشوند [۲۸]. یکی دیگر از فیلترهای نوری بر اساس رزونانس حلقه است؛ درواقع یک نمونه خاص از فیلترهای افتی است که در آن حلقه رزونانس انتخاب موج را انجام میدهد [۲۹]. مثال دیگری در این زمینه توسط رابینسن[۷] و ناکران[۸] انجامشده است. فیلتر آنها مانند هر فیلتر دیگر از یک پورت ورودی، یک پورت خروجی و یک حفره رزونانس ساختهشده بود. برای فیلتر کردن و انتخاب طولموج موردنظر، هشت نوع حفره به نامهای،شبه مربع، مربع سهچهارم، مربع، ششضلعی، دایرهای، بیضوی، لوزی و حفرههای بر پایه رینگهای حلقهای پیشنهادشده است [۳۰]. مشخصه بسیار شایع فیلترهای ذکرشده این است که هیچیک از آنها برای کاربردهای WDM و DWDM مناسب نیستند چون آنها به طیف وسیعی از طولموجها نیاز دارند.
اخیراً یک فیلتر نوری قابل تنظیم WDM مبتنی بر بلور فوتونی شبه-دوبعدی[۹] (Q2DPhC) پیشنهادشده است [۳۱]. که در آن بلور فوتونی دوبعدی با بلور فوتونی شبه-دوبعدی ترکیبشده است. بلور فوتونی شبه-دوبعدی انتخاب طولموج را انجام میدهد و با تغییر شعاع میلههای آنیک فیلتر قابل تنظیم، قابلدستیابی است.
برای دست بابی به یک فیلتر نوری قابل تنظیم برای دستگاههای DWDM، حفرههای رزونانس از بهترین گزینهها هستند. حفره رزونانس با ضریب کیفیت بالا (Q-factor) قادر به فیلتر کردن طولموج مطلوب با پهنای باند مناسب برای دستگاههای DWDM میباشد. همچنین با اعمال برخی تغییرات در ساختار این حفرهها میتوانیم فیلتر قابل تنظیم را به دست آوریم. این مکانیسم انتخاب طولموج در کار قبلی ما پیشنهادشده بود [۳۲] که در آن ما از آن برای طراحی یک دی مالتی پلکسر استفاده نمودیم. در حال حاضر در این مقاله قصد داریم یک فیلتر قابل تنظیم بر اساس یک حفره رزونانس L4 طراحی کنیم و ما پارامترهای مختلف را برای تنظیم طولموج خروجی فیلتر پیشنهادی موردبحث قرار خواهیم داد. سادگی فیلتر ما و کاربرد آن در قابلیت کاربردپذیری آن در DWDM، مهمترین مزیت فیلتر ما در مقایسه با فیلترهای فوق است.
بقیه این مقاله به شرح زیر است: در بخش ۲ مدلسازی و تحلیل نظری نشان دادهشده است. در این بخش نشان داده میشود که با انتخاب یک نقص مناسب بهعنوان یک حفره رزونانس با فیلتراسیون اصلاحشده با طراحی مناسب و انتخاب طولموج موردنظر، صورت میگیرد. در بخش ۳ شبیهسازی و نتایج فیلتر پیشنهادشده نشان داده خواهد شد. و درنهایت در بخش ۴، قسمت نتیجهگیری است.
آنالیز و مدلسازی تئوری
در حال حاضر بهترین روش برای استخراج خواص بلورهای فوتونی و مطالعه رفتار امواج الکترومغناطیسی در ساختارهای تناوبی مانند بلورهای فوتونی روشهای عددی است. اولین گام در طراحی و مطالعه ساختارهای مبتنی بر بلور فوتونی استخراج ساختار باند آن و به دست آوردن باند گپ فوتونی آنها است. یکی از رایجترین روشهای عددی برای محاسبه PBG این ساختارها، بسط موج تخت[۱۰] (PWE) [33] است. سرعتبالا محاسبه، مهمترین مزیت آن و محدود بودن محاسبه حالت ایستا از معایب آن است. ما از BandSolve برای انجام محاسبات PWE و استخراج ساختار باند و PBG ساختار پیشنهادی استفاده کردیم. یکی دیگر از روشها، محدود-تفاوت روش در حوزه زمان[۱۱] (FDTD) [34] است که توسط یی[۱۲] در سال ۱۹۶۶ پیشنهادشده است. FDTD یک روش قدرتمند و دقیق برای مطالعه و تحلیل مسئلههای الکترومغناطیسی مانند شبیهسازی ساختارهای مبتنی بر بلور فوتونی است. اینیک روش بسیار قدرتمند برای حل معادلات ماکسول[۱۳] در حوزه زمان است. در این مقاله، ما از FullWave برای انجام FDTD برای شبیهسازی و مطالعه رفتار امواج الکترومغناطیسی در فیلتر پیشنهادشده، استفاده کردیم.
در این مقاله هدف ما طراحی یک ساختار کامپکت برای فیلتر کردن طولموج است که تنها مبتنی بر بلورهای فوتونیک ۲ بعدی و بدون هیچگونه پیچیدگی اضافی باشد. بهعبارتدیگر، هدف ما کاهش کل اندازه فیلتر، پیچیدگیهای ساختار، پهنای باند و فاصله کانال در مقایسه باکارهای قبلی تنها با استفاده از بلورهای فوتونیک ۲ بعدی است. بنابراین ساختار پیشنهادی را برای به دست آوردن نتایج مطلوب، مدلسازی و تحلیل نمودیم. برای طراحی فیلتر پیشنهادشده ما PHC ششضلعی ۲ بعدی را که ساختار پایه آن در شکل ۱ نشان دادهشده است، پیشنهاد نمودیم. دارای ۹۰۰ حفر هوا است. تعداد منافذ هوا در جهت x و z (به ترتیب Nx و Nz) برابر ۳۰ است. ثابت شبکه a برابر با ۴۲۰ نانومتر است و شعاع حفرهها R برابر با ۱۱۵ نانومتر است. ضریب شکست مؤثر دیالکتریک پسزمینه ۷۳/۲ است. همانطور که قبلاً ذکر شد اولین قدم در طراحی و آنالیز ساختارهای مبتنی بر بلور فوتونی استخراج ساختار باند و پیدا کردن باند گپ فوتونی آن است.
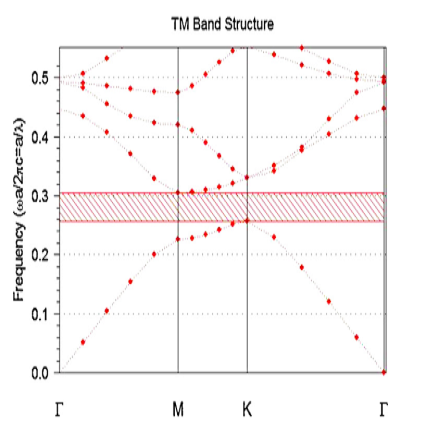
برای ساختار پیشنهادی، یک PBG فقط برای قطبش TE پیدا شد و در ناحیه تاریک در شکل ۲ نمایش داده میشود. حالت TE بهعنوان یکحالتی است که در آن پلاریزاسیون نور عمود بر حفرههای هوا تعریفشده است.
هیچ PBG برای حالت TM وجود ندارد. بنابراین تمام شبیهسازیها در حالت TE انجام میشود. ما در شکل ۲ مشاهده میکنیم که PBG در محدوده ا بهعبارتدیگر ی باشد.این به این معنی است که ساختار ما برای کاربردهای ارتباطی نوری مناسب است. فیلتر پیشنهادی در شکل ۳ نشان دادهشده است. همانطور که میبینیم فیلتر از سه قسمت اصلی تشکیلشده است. سمت اول که بهعنوان نقص مورب نامیده میشود، موجبر ورودی است که با حذف ۲۴ حفره در فرم مورب ایجاد میشود. آن موج نور دریافت شده را به سمت حفره رزونانس هدایت کند. سمت دوم و شاید مهمترین قسمت فیلتر، حفره رزونانس است که با حذف ۴ حفره هوا ایجاد میشود. حفره ما شامل دو نقص در گوشههای آنکه دارای شعاع Rc است ی باشد. علاوه بر این نقایص گوشهای، نقص دیگری را در حفره خودمان با جابهجایی پایین و بالای به ترتیب حفره وسطی بالا و پایین بهصورت L، معرفی مینماییم . همانطور که ذکر کردیم، مهمترین قسمت فیلتر ما حفرهای است که انتخاب طولموج و فیلتر را انجام میدهد.
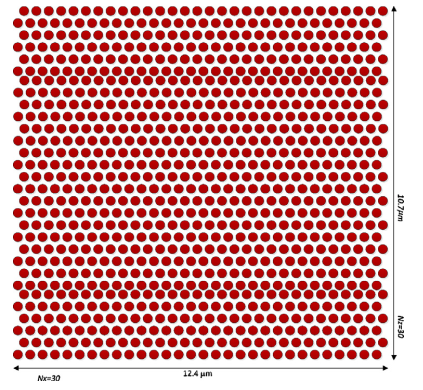
شکل ۱ : ساختار پایه بلور فوتونی ششضلعی دوبعدی
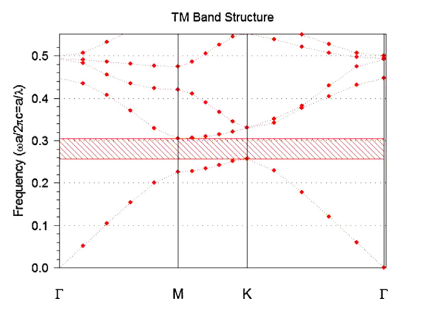
شکل ۲ : ساختار باند از ساختار پیشنهادی با R = 115 nm و a = 420 nm .
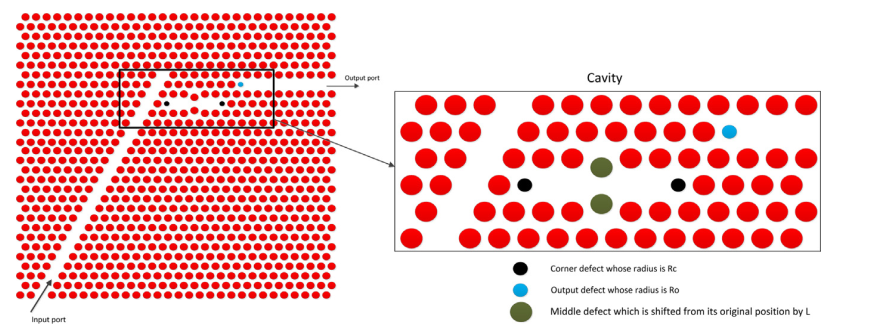
شکل ۳ : (a) طرح نهایی فیلتر پیشنهادشده ما و (b) حفره رزونانس با نقص آن
ما میتوانیم انتخاب طولموج را با سه عامل کنترل کنیم: (الف) تعداد حفرههای حذفشده حفره، (ب) شعاع نقصهای گوشه و (ج) اندازه جابهجایی L . اولین انتخاب (مورد الف)، انتخاب خوبی برای تنظیم نیست، زیرا برای انتخاب طولموج مناسب برای کاربردهای ارتباطی ما باید ۴ حفره را حذف کنیم. اما با تغییر شعاع نقاط گوشه، سرعت تغییر طول مؤثر حفره رزونانس بسیار پایین میآید، بنابراین طولموج انتخابشده بسیار آهسته جابهجا میشود. ما مشاهده میکنیم که تغییرات ۱۰ نانومتر در طول مؤثر حفره رزونانس باعث تغییر ۱ نانومتر در طولموج رزونانس میشود. بنابراین با ۵ نانومتر تغییر در شعاع نقاط گوشه میتوانیم طولموج انتخابشده را در ۱ نانومتر اندازهگیری کنیم. بنابراین دومین عامل برای فیلتر کردن مطلوب است. عامل سوم نیز برای تنظیم فیلتر مناسب است و با تغییر مقدار L ما میتوانیم فیلتر پیشنهادشده خود را تنظیم کنیم. علاوه بر این پارامترها، ما در مورد تأثیر دو پارامتر دیگر در رفتار فیلتر کردن فیلتر پیشنهادشده خود، بحث خواهیم کرد. ما نقص بالایی را با حرکت دادن بالا و پایین سوراخهای بالا و پایین در سمت راست و چپ نقص میانی معرفی میکنیم. درنهایت، شاخص انشعاب دیالکتریک را تغییر خواهیم داد و تأثیر آن بر خروجی فیلتر را بررسی خواهیم کرد.
درنهایت قسمت سوم فیلتر، موجبر خروجی است که هدف آن هدایت طولموج انتخابشده به سمت پورت خروجی و تکمیل فرآیند فیلتر کردن است. موجبر خروجی یک نقص خطی است که با حذف ۸ حفره هوا ایجاد میشود. یک نقص را در گوشهای از موجبر خروجی معرفی میکنیم که شعاع آن Ro است. Ro بر روی انتخاب طولموج تأثیری ندارد و فقط راندمان خروجی و پهنای باند طولموج خروجی را کنترل میکند.
شبیهسازیها و نتایج
همانطور که در بخش قبلی ذکر شد ساختار اصلی فیلتر ما یک بلور فوتونی ششضلعی دوبعدی است که از ۹۰۰ حفره هوا تشکیلشده است. تعداد منافذ هوا در جهت x و z (به ترتیب Nx و Nz) 30 است. ضریب شکست انبساط مواد دیالکتریک پسزمینه Neff = 2.۷۳ است. ثابت شبکه، شعاع منافذ هوا به ترتیب ۴۲۰ نانومتر و ۱۱۵ نانومتر است. طول ساختار در جهت x و z به ترتیب ۴/۱۲ و ۷/۱۰ متر است، بنابراین برش عرضی فیلتر پیشنهادشده ۶۸/۱۳۲ مترمربع است که برای استفاده در مدارهای مجتمع اپتیک مناسب است. برای رسیدن به پیکربندی فیلتر ما چندین حفره را برداشتیم و برخی از اصلاحات را انجام دادیم تا ساختار نشان دادهشده در شکل ۳ به دست آید. برای طراحی و شبیهسازی فیلتر ما، FullWave را برای انجام محاسبات FDTD مورداستفاده قراردادیم. همانطور که ذکر شد قسمت اصلی فیلتر حفره رزونانس است و همچنین ما اشاره کردیم که برای تنظیم طولموج انتخابی فیلتر بهترین گزینهها عبارتاند از شعاع نقص گوشه حفره، Rc و جابهجایی L حفره میانی بالا و پایین از حفره. بنابراین ما تأثیر خود را بر رفتار فیلترینگ و طولموج خروجی فیلتر پیشنهادی بررسی نمودیم.
در کنار این نقصها، نقص دیگری نیز وجود دارد، که نقص گوشهای از موجبر خروجی (Ro) میباشد. شبیهسازیها نشان میدهد که Ro هیچ تأثیری در انتخاب طولموج ندارد و تنها راندمان خروجی و پهنای باند طولموج خروجی را کنترل میکند. شبیهسازی نشان داد که با افزایش Ro بازده خروجی و پهنای باند افزایش مییابد و با کاهش Ro نیز بازده خروجی و پهنای باند کاهش مییابد. ازآنجاکه هدف ما حداکثر بازده خروجی و حداقل پهنای باند است – برای داشتن حداکثر فاکتور-Q – ما باید یک مقدار بهینه برای Ro پیدا کنیم. با آزمونوخطا، ما دریافتیم که مقدار مطلوب Ro = 73 nm ست.
در فیلتر پیشنهادی ما مقادیر Rc، L و Ro به ترتیب ۸۸ نانومتر، ۶۸ نانومتر و ۷۳ نانومتر است. طیف خروجی فیلتر با این ویژگیها در شکل ۴ نشان دادهشده است. شکل ۴ نشان میدهد که ساختار در فیلتر نوری که تنها طولموجهای ۱۵۶۷ نانومتر، پهنای باند به ۷/۰ نانومتر است و فاکتور- Q 238 است، عمل میکند. در زیر ما اثر Rc و L را بر طولموج خروجی فیلتر بررسی خواهیم کرد و نشان خواهیم داد که میتوان فیلتر را ا تغییر این دو عامل، تنظیم کرد. ابتدا اثر Rc را بررسی میکنیم. با تغییر Rc طول مؤثر حفره تغییر میکند بهطوریکه باعث جابهجایی طولموج رزونانس میشود. برای جدا کردن اثر Rc از L ما L را ثابت نگهداریم و Rc را تغییر دهیم و سپس طولموج خروجی فیلتر را بررسی کنیم. فرض کنیم که L = 70 نانومتر و Ro = 73 نانومتر است. سپس طولموج خروجی برای Rc برابر با ۶۲، ۷۷، ۷۲، ۷۷، ۸۲، ۸۸، ۹۲ و ۹۷ نانومتر اندازهگیری شد. نتایج در شکل ۵ و جدول ۱ نشان دادهشده است. ما میبینیم که با افزایش Rc، طولموج خروجی به مقدار کمتری تغییر میکند.

شکل ۴ : خروجی فیلتر پیشنهادشده برای Rc = 88 nm، L = 68 nm و Ro = 73 nm.
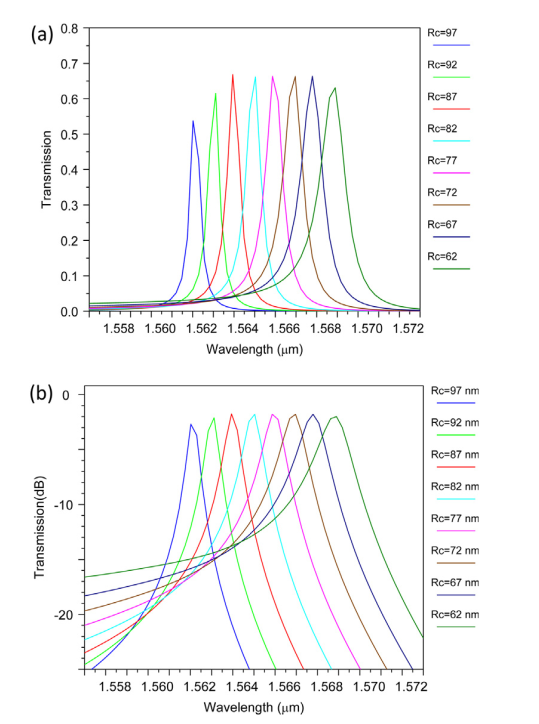
شکل ۵ : خروجی فیلتر برای L = 70 nm، Ro = 73 nm و مقادیر مختلف Rc (a) مقیاس خطی و (b) مقیاس dB.
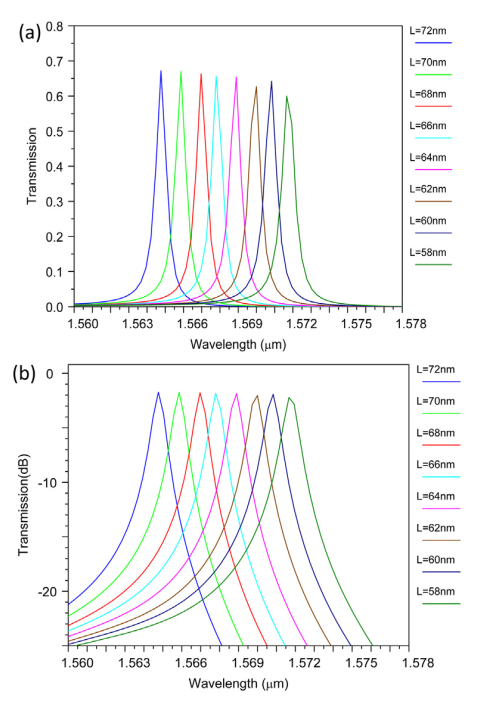
شکل ۶ : خروجی فیلتر برای Ro = 73 nm، Rc = 88 nm و مقادیر مختلف L (a) مقیاس خطی و (b) مقیاس dB.
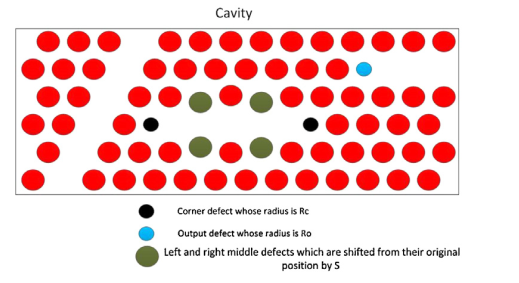
شکل ۷ : حفره اصلاحشده با نقایص جدید (جابهجایی S).
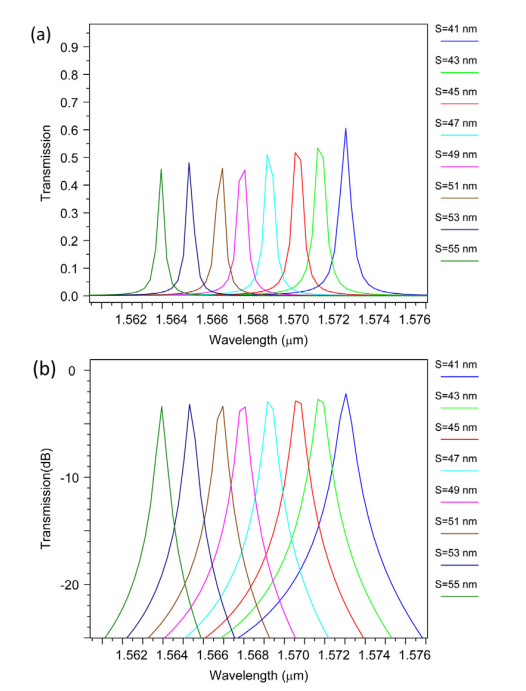
شکل ۸ : خروجی فیلتر برای, L=0 Ro = 73 nm، Rc = 88 nm و مقادیر مختلف L (a) مقیاس خطی و (b) مقیاس dB.
جدول ۱ : پارامترهای مهم فیلتر ما برای L = 70 nm، Ro = 73 nm و مقادیر مختلف Rc
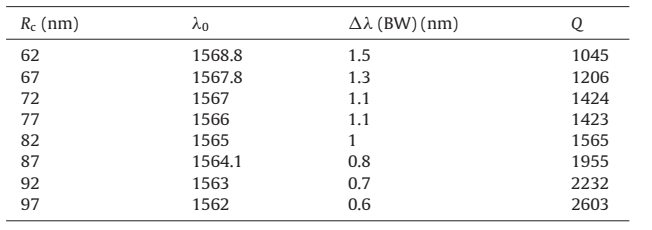
جدول ۲ : پارامترهای مهم فیلتر ما برای Rc = 88 nm، Ro = 73 nm و مقادیر مختلف L
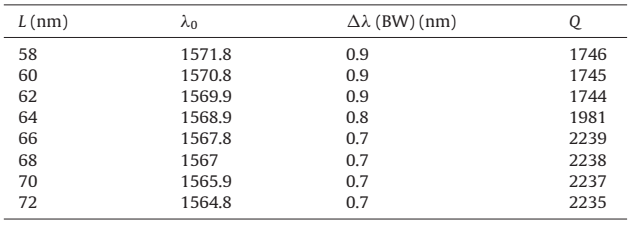
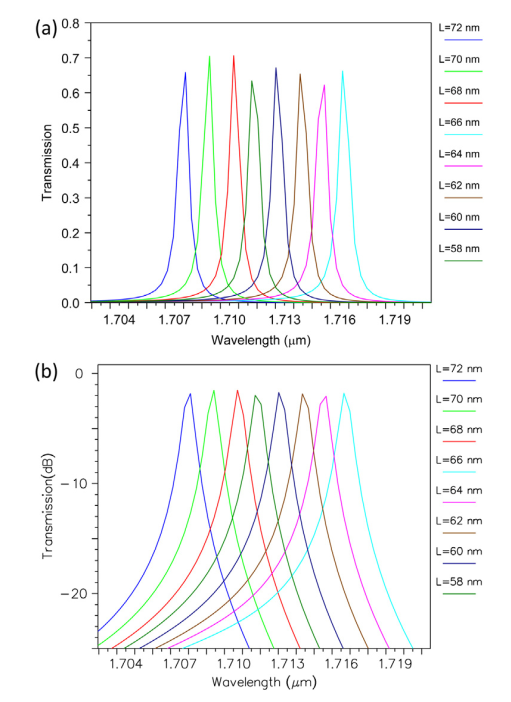
شکل ۹ : خروجی فیلتر برای, Ro = 73 nm، Rc = 88 nm و مقادیر مختلف L برای n=3 (a) مقیاس خطی و (b) مقیاس dB
سپس اثر L را بر طولموج خروجی فیلتر بررسی نمودیم. اکنون برای جداسازی اثر L از Rc، Rc را ثابت نگه میداریم و L را تغییر میدهیم. فرض کنید Rc = 88 nm و Ro = 73 nm میباشد. سپس طولموج خروجی برای L برابر با ۵۸، ۶۰، ۶۲، ۶۴، ۶۶، ۶۸، ۷۰ و ۷۲ نانومتر اندازهگیری شد. نتایج در شکل ۶ و جدول ۲ نشان دادهشده است. ما میبینیم که با افزایش L طولموج خروجی به سمت طولموجهای پایینتر جابهجا میشود.
در حال حاضر بهجای نقص میانی،ما بالا و پائین حفرهها های بالا و پایین را در سمت راست و چپ نقص میانی بهصورت S جابهجا میکنیم و اثر آن را بر طولموج خروجی فیلتر بررسی میکنیم. بنابراین حفره به نظر میرسد مانند شکل ۷ باشد. ما فرض میکنیم که Rc = 88 nm، Ro = 73 nm و L = 0 است، سپس طولموج خروجی را برای S برابر با ۴۱، ۴۳، ۴۵، ۴۷، ۴۹، ۵۱، ۵۳ و ۵۵ نانومتر اندازهگیری میکنیم. نتایج در شکل ۸ و جدول ۳ نشان دادهشده است. ما میبینیم که با افزایش طولموجهای S خروجی به سمت طولموجهای پایینتر جابهجا میشود. مقایسه نتایج پارامتر S با پارامتر L نشان میدهد که فیلتر تنظیم بر اساس کانال نتایج S با فاکتور-Q بالاتر از پارامتر L میدهد، اما نسبت به آن جابهجایی آن کمتر از نقص L است.
درنهایت فرض کنیم که ضریب شکست مؤثر فیلتر پیشنهادی ما ۳ بهجای ۷۳/۲ است. سپس ما اندازهگیریها را برای مقادیر مختلف L انجام میدهیم. بنابراین برای Rc = 88 nm، Ro = 73 nm، S = 0 و L برابر با ۵۸، ۶۰، ۶۲، ۶۴، ۶۶، ۶۸، ۷۰ و ۷۲ نانومتر، ما طولموج خروجی را اندازهگیری میکنیم. نتایج بهدستآمده در شکل ۹ و جدول ۴ نشان دادهشده است. این نتایج نشان میدهد که تغییر ضریب شکست مواد دیالکتریک بر طولموج خروجی فیلتر پیشنهادی تأثیر معنیدار دارد، بهطوریکه ۲۳/۰ افزایش ضریب شکست ماده دیالکتریک باعث افزایش بیش از ۱۵۰ نانومتری در طولموج خروجی فیلتر میشود.
نتیجهگیری
در این کار یک فیلتر تنظیمی فوقالعاده کامپکت مبتنی بر یک بلور فوتونی ششضلعی ۲ بعدی پیشنهادشده است. انتخاب طولموج و فیلتر کردن توسط یک حفره رزونانس انجام میشود. اندازه فوقالعاده کوچک و سادگی فیلتر پیشنهادی آن را برای مدارهای مجتمع اپتیک مناسب میسازد. ما نشان دادیم که با تغییر Rc و L میتوانیم فیلتر پیشنهادی را تنظیم کنیم و طولموجهای موردنظر را فیلتر نماییم. ما میتوانیم ادعا کنیم که فیلتر ما برای کاربردهای ارتباطی نوری WDM و DWDM مناسب است.
- Wavelength Division Multiplexing (WDM) ↑
- Dense Wavelength Division Multiplexing (DWDM) ↑
- تداخل سنج وسیله ای برای اندازیه گیری فواصل بسیار کوچک از طریق تقسسیم و هدایت نور در مسیرهای جداگانه و سپس ترکیب دوباره ی آنها، اختلاف طول مسیر به صورت الگوی تداخل نوری نمایش داده می شود یک کاربرد آن در اندازه گیری لایه های بسیار نازک است. ↑
- photonic band gap (PBG) ↑
- photonic crystals (PhCs) ↑
- Add-Drop ↑
- Robinson ↑
- Nakkeran ↑
- Quasi-2D PhC ↑
- Plane Wave Expansion (PWE) ↑
- Finite Difference Time Domain (FDTD) ↑
- Yee ↑
- Maxwell’s equations ↑